粘弹性破裂可以超越传统极限速度

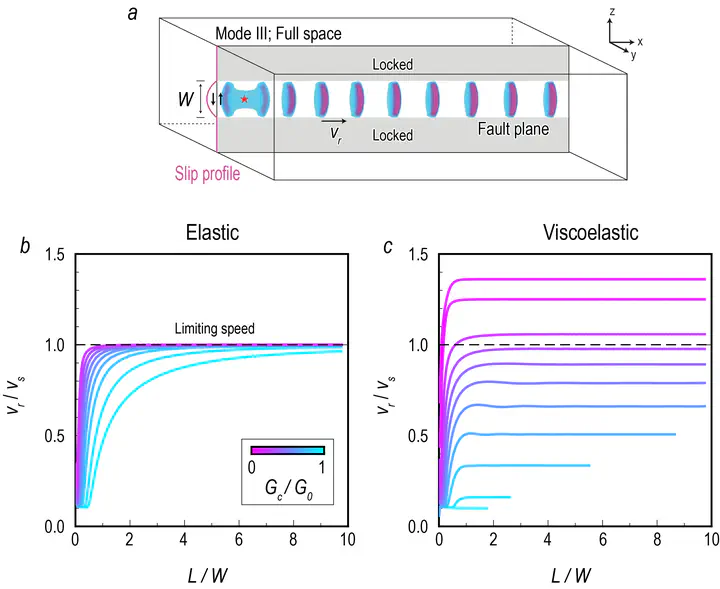
Classical theories using linear elasticity predict that crack propagation is bounded by a limiting speed, beyond which the energy balance becomes unphysical. Recent experiments in viscoelastic materials demonstrated that both tensile and frictional crack propagation can exceed classical speed limits. However, the fundamental physics governing unbounded rupture speeds are still unclear. Numerical simulations show that frictional ruptures in viscoelasticity can propagate at a continuum of terminal speeds that are not bounded by the classical speed limit. All simulated rupture speeds are predicted by the newly developed theory of fracture mechanics incorporating viscoelasticity via the principle of energy balance. In addition to the ratio of the fracture energy to the static energy release rate that can be used to uniquely predict the rupture propagation in linear elasticity, the scales of characteristic lengths in viscoelasticity also govern the energy balance. Beyond the classical speed limit, the energy balance becomes independent of any macroscopic length and is controlled only by the local properties around the rupture tip. These numerical and theoretical findings fundamentally advance our understanding of dynamic rupture propagation.